GIMNAZIJA
AKTUELNO
Forum
SAJTOVI
ZANIMLJIVO
Izvod funkcije
(Matematika)
Lajbnic i Njutn radili su gotovo u istom vremenskom periodu, nezavisno jedan od drugog i obojica dosli do pojma izvoda. Pojam izvoda nastao je krajem XVII veka u vezi sa izučavanjem neravnomernih kretanja. Preciznije, pomoću izvoda je bilo moguce uvesti pojam trenutne brzine pravolinijskog kretanja. Uopšte, pomocu izvoda moze se predstaviti brzina promene veličina koje se neravnomerno menjaju (temperature tela,električne struje...). Pojam izvoda pojavio se i u vezi sa nalaženjem tangente krive u datoj tački.U tom smislu, zauzima značajno mesto u matematici i njenim primenama.
Priraštaj nezavisno promenljive i priraštaj funkcije
Neka je y=ƒ(x) kriva u ravni xOy, M0(x0,y0) proizvoljna fiksirana tačka na toj krivoj i M(x,y) još jedna tačka te krive,različita od M0. Priraštaj nezavisno promenljive je broj
Δx=x-x0,
a priraštaj funkcije ƒ u tački x0 je broj
Δƒ(x0)=ƒ(x)-ƒ(x0)=ƒ(x0+Δx)-ƒ(x0).
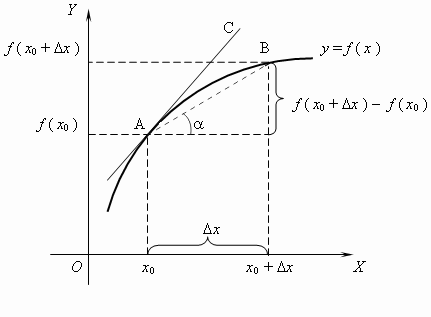
Prava MM0 je sečica date krive. Nagib te krive odreðen je njenim koeficijentom pravca, koji je jednak:
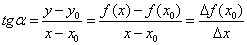
Koficijent pravca sečice jednak je količniku priraštaja funkcije i priraštaja nezavisno promenljive.
Prvi izvod
Prvi izvod ƒ'(x) funkcije ƒ u tački x0 je konačna granična vrednost:
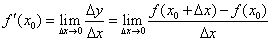
Izvod funkcije ƒ u tački x0 je broj koji je jednak koeficijentu pravca tangente te funkcije u tački M0(x0,y0).
Tablica izvoda elementarnih funkcija
Funkcija 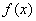 |
Izvod 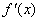 |
Važi za |
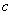 -konstanta -konstanta |
0 | 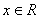 |
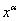 |
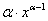 |
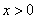 za za
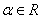 |
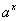 |
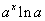 |
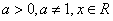 |
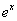 |
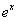 |
|
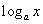 |
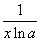 |
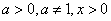 |
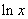 |
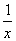 |
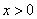 |
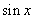 |
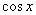 |
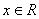 |
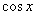 |
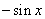 |
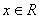 |
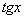 |
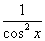 |
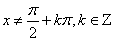 |
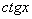 |
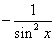 |
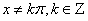 |
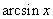 |
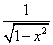 |
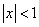 |
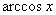 |
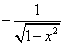 |
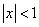 |
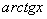 |
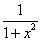 |
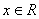 |
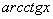 |
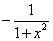 |
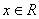 |
Osnovne teoreme o izvodu
Ako su ƒ i g diferencijabilne funkcije u tački x i c-konstanta, tada vazi:
Izvod zbira i razlike
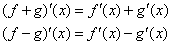
Izvod proizvoda i količnika
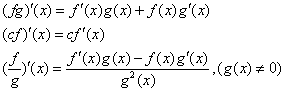
Izvod slozene funkcije
Ako je funkcija y=ƒ(x) diferencijabilna u tački x, a funkcija z=g(y) diferencijabilna u tački y=ƒ(x),tada je slozena funkcija z=g(ƒ(x)) diferencijabilna u tački x i vazi:
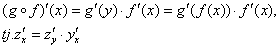
Drugi izvod i izvodi višeg reda
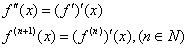
Tangente i normale krive y=ƒ(x)
Jednačina tangente
Jednačina tangente krive l, koja je grafik funkcije y=ƒ(x) u tački (x0,y0) ∈ l je:
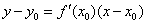
Jednačina normale
Jednačina normale krive l, koja je grafik funkcije y=ƒ(x) u tački (x0,y0) ∈ l je:
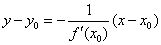
Primena izvoda pri ispitivanju funkcija
Monotonost funkcije
Neka je funkcija ƒ diferencijabilna u intervalu (a,b) (tj. neka ima izvod u svakoj tački tog intervala). Ako je ƒ´(x) > 0, za svako x ∈ (a,b), tada je funkcija ƒ rastuca u tom intervalu. Ako je ƒ´(x) < 0, za svako x ∈ (a,b), onda je funkcija ƒ opadajuca u tom intervalu.
Ekstemne vrednosti funkcije
Neophodan uslov za postojanje lokalnog ekstemuma: Izvod funkcije ƒ u tački c lokalnog ekstemuma, u kojoj je funkcija ƒ diferencijabilna jedank je nuli.
Dovoljan uslov za postojanje lokalnog ekstremuma:
- Neka funkcija ƒ ima u tački x0 prvi izvod koji je jednak nuli i neka u toj tački ima drugi izvod ƒ″(x0). Tada, ako je ƒ″(x0) < 0 (ƒ″(x0) > 0), funkcija ƒ ima u x0 tačku strogog lokalnog maksimuma (minimuma).
- Neka je ƒ(x) neprekidna funkcija, diferencijabilna u nekoj okolini tačke x0, osim, možda, u x0. Ako ƒ´(x0) menja znak kada x prolazi kroz x0, tada je x0 tačka strogog lokalnog ekstremuma. Ako je ƒ´(x) < 0 za x < x0 i ƒ″ > 0 za x > x0, tada je x0 tačka lokalnog minimuma, a ako je ƒ´ > 0 za x < x0, a ƒ″(x) < 0 za x > x0, tada je x0 tačka lokalnog maksimuma.
Konveksnost i konkavnost
Neka funkcija ƒ(x) : (a,b)→ R ima u svakoj tački x ∈ (a,b) drugi izvod. Funkcija ƒ je konveksna na (a,b) ako i samo ako je ƒ″ > 0 za sve x ∈ (a,b). Funkcija ƒ je konkavna na (a,b) ako i samo ako je ƒ″ < 0 za sve x ∈ (a,b).
Prevojne tačke
Neka je funkcija ƒ diferencijabilna u nekoj okolini tačke x0 i ima drugi izvod u toj okolini, osim, možda, u tački x0. Ako ƒ″(x) menja znak pri prolazu argumenta kroz tačku x0, onda je (x0,ƒ(x0)) prevojna tačka krive y=ƒ(x).
Lopitalova teorema
Teorema 1: Neka su funkcije ƒ(x) i g(x) definisane u intervalu (a,b],
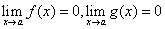 , u intervalu (a,b] postoje konačni izvodi ƒ´(x) i g´(x), pri čemu je g´(x) ≠ 0 i, najzad, postoji(konačan ili ne) limes i
, u intervalu (a,b] postoje konačni izvodi ƒ´(x) i g´(x), pri čemu je g´(x) ≠ 0 i, najzad, postoji(konačan ili ne) limes i
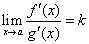 . Tada je
. Tada je ![]() .
.
Teorema 2: Neka su funkcije ƒ(x) i g(x) definisane u intervalu (a,b],
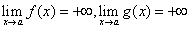 , u intervalu (a,b] postoje konačni izvodi ƒ´(x) i g´(x), pri čemu je g´(x) ≠ 0 i, najzad, postoji(konačan ili ne) limes i
, u intervalu (a,b] postoje konačni izvodi ƒ´(x) i g´(x), pri čemu je g´(x) ≠ 0 i, najzad, postoji(konačan ili ne) limes i
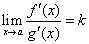 . Tada je
. Tada je ![]() .
.
Teoreme 1 i 2 važe i kada je a= +∞ ili a= -∞.
Редовни
- Српски
- Мађарски
- Српски-нематерњи
- Енглески
- Немачки-1
- Немачки-2
- Француски
- Руски
- Латински
- Психологија
- Филозофија
- Социологија
- Устав
- Географија
- Историја
- Биологија
- Хемија
- Физика
- Математика
- Информатика
- Ликовно
- Музичко
- Физичко
Изборни
- Веронаука
- Грађанско